Not everyone thinks of cats as being big helpers, but mine seems to very much enjoy helping me with my workouts — with push-ups especially:
 Some might say that she is actually hindering the doing of push-ups, which is technically true . . . but since the whole point of the exercise is, well, to exercise, the extra weight is ultimately helpful.
Some might say that she is actually hindering the doing of push-ups, which is technically true . . . but since the whole point of the exercise is, well, to exercise, the extra weight is ultimately helpful.And it actually makes a difference! At least, it feels like it makes a difference. Despite her affinity for cookies (among other things), she only weighs about nine percent as much as I do; yet, push-ups feel more than nine percent harder when she’s up there. Is that just my perception? Or is there something about how the weight is distributed that gives her contribution a disproportional effect?
I decided to investigate the matter, breaking it up into three key questions:
1. How much force is actually required to do a push-up?
2. How does the addition of a medium-sized feline passenger increase the required force?
3. How much does additional force change the difficulty of the exercise — or, relatedly, the number of push-ups that one should expect to be able to do?
Part 1: Standard push-ups
The amount of weight on your hands when you do a push-up has been calculated before, and it can easily be measured experimentally — e.g., by putting your hands on a scale. However, the error bar in the scale measurement is potentially fairly large, and I was interested in a more rigorous calculation of the body’s center of mass, as well the option of treating the arms separately (for later use in other problems). Therefore, I decided to try solving the problem using body segment data (how much different body parts weigh, how long they are, and where their centers of mass are).
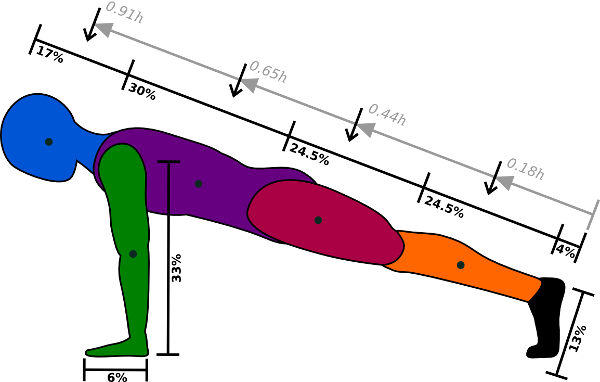
First, here’s a table showing how a person’s body weight is typically distributed among six different segments:
| body segment | percent of body weight |
| head and neck | 6.8% |
| trunk | 43% |
| upper leg | 14.5% each |
| lower leg | 4.6% each |
| arm and hand | 4.7% each |
| foot | 1.3% each |
Next, here is a diagram showing the dimensions of those segments and the locations of their centers of mass when one is in “push-up position”:
The centers of mass of each segment are indicated by dots. Dimensions (in black) are given as a percentage of total height (distance from soles of feet to top of head when standing straight up). The gray numbers in italics indicate the heights (when standing) to the four indicated centers of mass as a fraction of total height h. For example, 43 percent of your total body weight is in your trunk, which is 30 percent as long as you are tall and whose center of mass is located 0.65*h above the ground when you are standing.
Now, consider the following observations about someone holding a static push-up position1:
- The vector sum of all the forces on the body is zero. In other words, the person is neither sinking into the floor nor floating up off of it. The downward force of gravity is balanced by upward forces from the floor on one’s hands (which is what we want to calculate) and on one’s feet.
- The total torque around any point of the body is zero. In other words, the person is neither rotating forward (into a headstand) nor backward (onto their feet).
These two pieces of information, plus the data above, give us all the information we need to solve the problem.
However, there is one part that is slightly messy: the calculation of the overall center of mass. The fact that the arms are extended “out” from the body means that the center of mass is “pulled away” from the line along which the rest of the body (except for the feet) lies. Thus, the center of mass calculation requires us to take into account the angle between the arms and the rest of the body. This is totally doable, of course; it’s just a little inelegant.
A more intuitive approach, in my opinion, comes from considering the implications of three more statements about this system:
- All of the weight of the arm segments is on the arms.2
- All of the weight of the feet segments is on the feet.2
- The distribution of the weight of the rest of the body (the “straight” section) onto hands versus feet depends only on where along the section its center of mass is located. No angles need to be involved.3
The math is now a lot simpler; since the head and neck, torso, and legs are all collinear, the location ![]() of their collective center of mass is just a one-dimensional weighted average of the locations of the individual centers of mass (which we know from the diagram above):
of their collective center of mass is just a one-dimensional weighted average of the locations of the individual centers of mass (which we know from the diagram above):
(1) 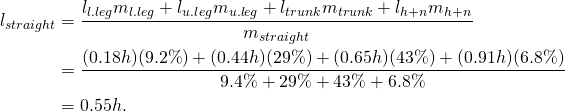
In other words, the center of mass of the straight section of the body is 55 percent of one’s height when standing — or roughly a couple centimeters below that part of your hip bone that sticks out in front.
We can now calculate what percent of the weight of the straight section is held up by the hands (rather than the feet):
(2) ![]()
Taking into account that the straight section of the body represents 88 percent of the total body weight, then adding the weight of the arms (each representing 4.7 percent of the total body weight), we get:
(3) 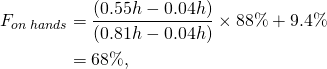
which is in very good agreement with measured values.
Part 2: Cat-assisted push-ups
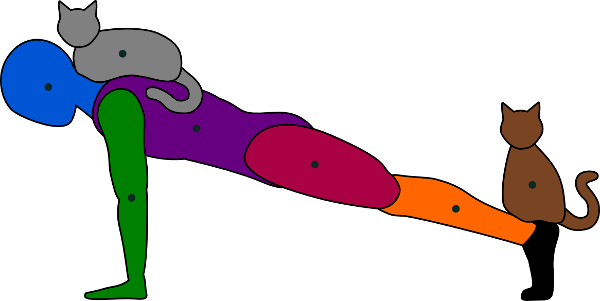
The next question is how much that changes when there’s a cat helping out. As one might surmise from the previous discussion, that depends on where the cat is located. Consider, for illustrative purposes, the following two theoretical feline “helpers”:
The brown cat, with its center of mass almost directly above the feet, isn’t having any appreciable effect on the push-ups (except for any discomfort that may be involved in having claws digging into one’s heels). The gray cat, on the other hand, centered directly over the shoulders, contributes its entire body weight to the cause of helping increase the effectiveness of each push-up. (Note that it could contribute even more if it perched on the person’s head, but we’ll leave that investigation as an exercise for the reader.)
If the gray cat weights nine percent as much as the person, the force on the hands is now increased to 68 + 9 = 77 percent of the person’s total body weight — an increase of 9/68 = 13 percent from the original, cat-free force.
Part 3: Push-up difficulty
The last question is how much the extra weight can be expected to increase the difficulty of the exercise, or alternatively — since “difficulty” isn’t immediately quantifiable — to decrease the number of push-ups in a set.
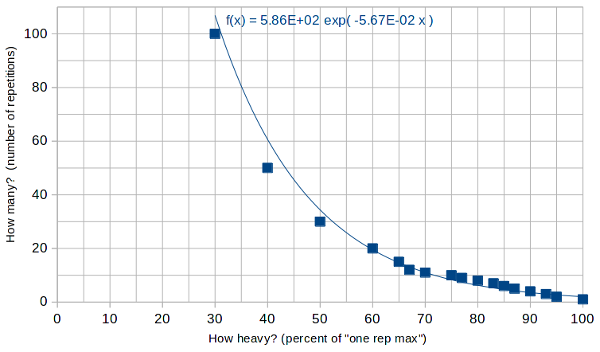
Conveniently, the website speedendurance.com has a table relating repetitions to weight relative to one’s “one rep max” (i.e., the maximum load under which on can perform a given exercise exactly one time; to do it again requires resting in between).
Here’s a graph of the data:
I’ve also added an exponential curve that fits the data points fairly well (if not perfectly) and allows us to make a more general calculation of how ![]() (reps with cat) can be expected to compare to
(reps with cat) can be expected to compare to ![]() (reps without cat)
(reps without cat)
(4) 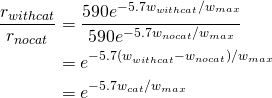
where ![]() is the amount of weight being lifted without the cat,
is the amount of weight being lifted without the cat, ![]() is the contribution from the cat,
is the contribution from the cat, ![]() is the amount of weight being lifted with the cat, and
is the amount of weight being lifted with the cat, and ![]() is the maximum load one can successfully “push up”.
is the maximum load one can successfully “push up”.
As it turns out, one’s own body weight cancels out of the equation entirely! That is, it doesn’t strictly matter how large the cat’s contribution is in comparison to one’s own body weight (or the 68 percent of that that is typically lifted in a standard push-up); all that matters is how the cat’s contribution compares to the maximum possible load.
Unfortunately, I don’t actually know what the maximum load is that I can lift in a push-up. However, I do have two other reference points:
- I usually do push-ups in sets of 35 and find this to be an effective work-out. On the graph above, 35 reps corresponds to 50 percent of one’s one rep max, suggesting I should be able to manage a push up with at most twice that — i.e., 136 percent of my body weight. This is probably too generous, but let’s use it as an upper bound for
 .
. - I know that my one rep max for a bench press (a similar motion to a push-up) is not that high. Last I checked, I could just barely bench press my body weight one time; that is, my one rep max for the bench press was equal to my body weight. This would suggest that I ought to be doing push-ups in much smaller sets (12 instead of 35), which seems like far too few, but we can use this as a lower bound for
 .
.
Thus, if ![]() is between 100 and 136 percent of my body weight, and knowing that
is between 100 and 136 percent of my body weight, and knowing that ![]() is equal to nine percent of my body weight, we can use the equation above to calculate that
is equal to nine percent of my body weight, we can use the equation above to calculate that ![]() = 0.60-0.69. That is, I can expect to do only about 2/3 as many push-ups with the cat as without — not a small difference!
= 0.60-0.69. That is, I can expect to do only about 2/3 as many push-ups with the cat as without — not a small difference!
Even if I were to get much stronger, to the point where I could do a push-up with more than 200 percent of my body weight on my hands, I could still expect a noticeable difference with the addition of my cat: a decrease in the reps per set from 100 to 78. On the other hand, if I were to get weaker, to the point where I could only lift 75 percent of my body weight in a push-up, adding my cat would reduce the number of repetitions in a set from five down to just one.
Conclusion
To summarize, we’ve figured out the following:
- A standard push-up involves lifting 68 percent of one’s body weight.
- The additional weight contributed by a feline passenger depends on where the cat is located and can indeed be more than the cat actually weighs on its own.
- Push-ups can be expected to be noticeably harder; interestingly, how much harder doesn’t depend on how much you weigh but rather just on how much you can lift (and, of course, on how massive the cat in question happens to be).
Footnotes:
1.) Obviously, actually doing a push-up is not exactly the same thing as holding a push-up position. During a push-up, both of the “equilibrium conditions” are false. That is, the total sum of forces on the body is not zero, because the body’s center of mass moves down and up. Similarly, the total torque is also not zero, because the body rotates forward somewhat on the downward motion and backward somewhat on the upward motion, as the height of the shoulders above the floor decreases and increases while the height of the ankles above the floor is constant. These average out over the cycle of doing a push-up, though, so the static analysis does the job nicely.
2.) Note that these two statements are only true because the arm and leg segments are vertical and the ground is flat; thus the upward forces from the ground directly oppose the downward gravitational force from those segments’ centers of mass. One particularly illustrative counter-example is as follows: If instead of having your shoulders directly over your hands, you instead lean them far enough forward that your overall center of mass is now directly over your hands, there will be no weight at all left on your feet. This is called a “planche”.
3.) This is a general thing that you can prove by looking at torque balance. It means that if you and your friend are holding up opposite ends of, say, a folded-up table (or anything else that’s long and thin), holding your end higher or lower doesn’t change what fraction of the weight you’re supporting.