A new year usually means it’s time for a new calendar. One can opt for 12 months of natural parks or scenes from a favorite film or TV show, 365 days of political cartoons or origami projects, or so many others. The possibilities are nigh endless.
But what if you really liked last year’s calendar? Maybe it already had the perfect mix of paintings from your favorite artist, or maybe there was a different classic family photo on each month, and you’d be happy to see them all again. Suppose you just used the calendar for keeping track of which date fell on which day of the week (rather than, say, writing down appointments on it), so that it’s still pristine. Why not just hang onto it and hang it up again the next time it’s accurate? How long will you have to wait?
In other words, how long is it until the next year in which all the dates fall on the same days of the week? Let’s call this having the “same calendar”. (Note that I’m neglecting moon cycles and holidays that are based on the lunar calendar, such as Easter and Ramadan, as including these makes for a much more complicated and — on the human time scale, less interesting — problem.) Two years have the same calendar if two conditions are both fulfilled:
- They both start on the same day of the week.
- They both have the same number of days.
This means that we have 14 different calendars altogether: two lengths (either 365 days for non-leap years, or 366 days for leap years) and seven different days of the week on which they can start. Do all of these occur? And in what order do they occur? To visualize the problem, represent these by two concentric rings of seven points each. Then trace out the sequence in which they come up:
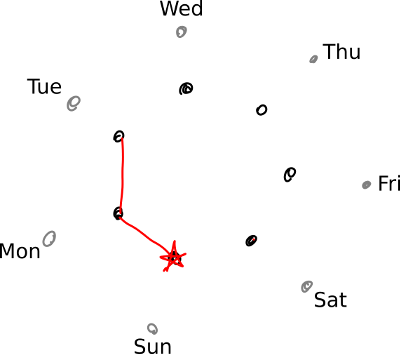
Our starting point is 2017 (represented by the red star), which began on a Sunday and ended on a Sunday, since a standard (non-leap) year is one day longer than being exactly 52 weeks long (because 52 times 7 equals 364). Mathematically, this is written 
, and the “mod” represents the modulo operation — i.e., a more compact say of saying, “What is the remainder when I divide 365 by 7?” As a result, 2018 started on a Monday, and 2019 will start on a Tuesday.
2020 will start on a Wednesday, but it’s a leap year, so we switch to the outer circle of points (representing leap year calendars). Also, since leap years are 366 days long, and 
, 2021 will start not on a Thursday but rather on a Friday. (The skipping ahead in the week, relative to the usual pattern, is probably how the term “leap year” originated in the first place.)
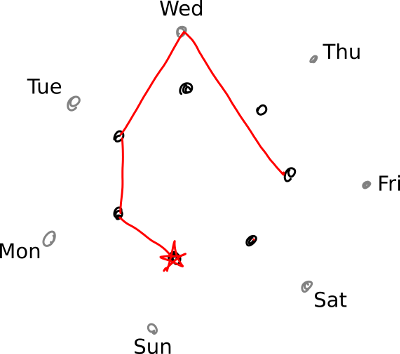
From this point, it’s clear that in another two years, we will back at the point we started. Thus, the 2017 calendar will be ready for a reprise six years later, in 2023.
This isn’t a very general answer, though; that is, we can’t say that you always wait six years to use a calendar again. If we keep going around the circle, we won’t be retracing our path yet, since 2024 will be a leap year. Because 2017 followed a leap year, we will first be retracing our steps when we end up back at the red star after having immediately come from a leap year.
Let’s keep going around until this happens, keeping track of how many times we’ve past our starting point by changing colors:
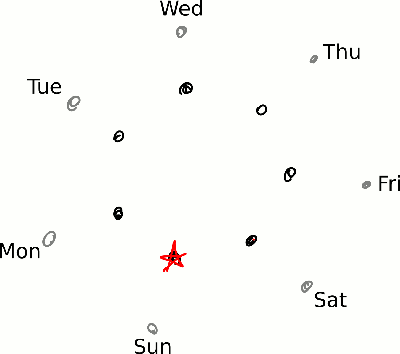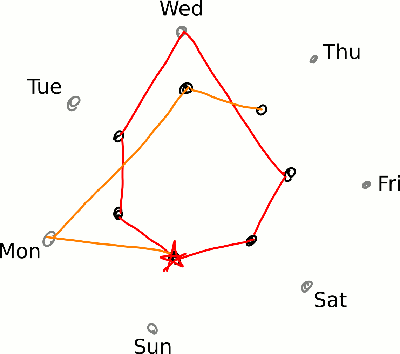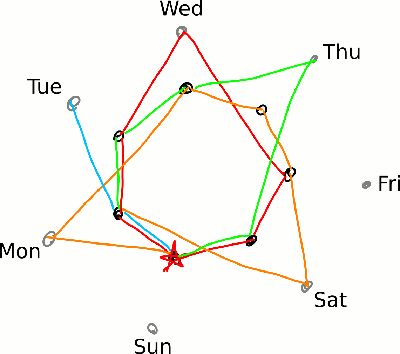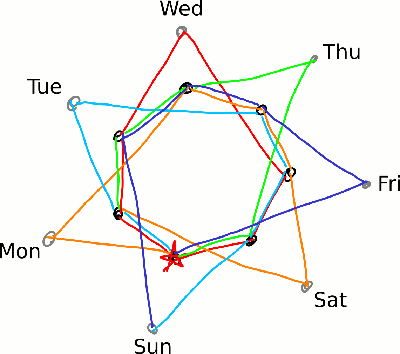
We end up with 28-year cycle; each leap year happens once and each non-leap year happens three times. We can also now see that there are three possibilities for how long it will be until a calendar can be used again:
- It could be as short as 6 years — i.e., our original answer. This is the case when the previous year was a leap year.
- More likely (twice as often), it will be 11 years. (On the next time around the circle, that calendar will be skipped either because it’s time for a leap year or because the previous year was a leap year.)
- For leap years, it will be 28 years.
Thus, if your favorite family photo calendar was from 2016, it will be time to dust it off again in 2044.
We can also draw an alternate, more elegant diagram, in which each “common” year (non-leap year) is represented by a cluster of three points: one for when it comes right after a leap year, one for when it occurs right before a leap year, and one for when it occurs halfway between leap years:
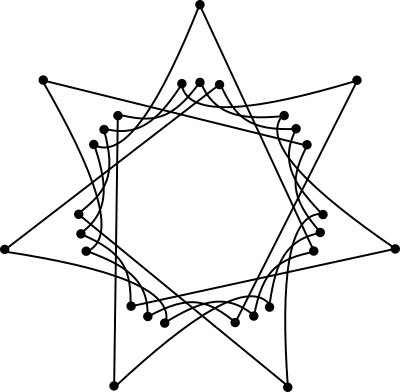
This makes the 28-year period of the cycle more evident, but it does so at the expense of making it less obvious that all three points in each cluster in the inner circle all have the same calendar.
Now, 28 years isn’t actually that short relative to 100 years — i.e., the length of time that most often passes between “skipped” leap years. (In the Gregorian calendar, a year is a leap year if it’s divisible by 4, but not if it’s divisible by 100, unless it’s divisible by 400.) Thus, it’s worth considering how a skipped leap year affects our calendar cycle. Each century consists of three full 28-year cycles, totaling 84 years, plus a fourth partial cycle, which we can illustrate like this:
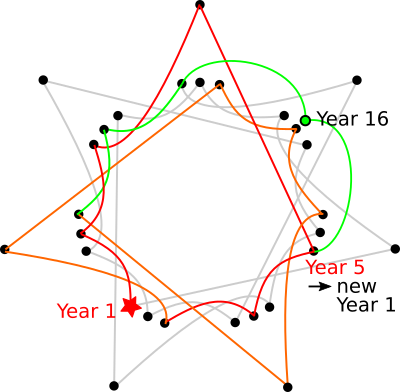
In a standard cycle, Year 16 is a leap year, but this time it is instead a common year that repeats sooner than it normally would (after 6 years instead of 11), as does the the year after. The last 13 years of that 28-year cycle are skipped, so are the first four of the next cycle, as what was Year 5 in the previous century becomes Year 1 in the new century. For example, 1 January 2001 was a Monday, which means that 1 January 2005 was a Saturday, and 1 January 2101 will be a Saturday, too.
Last but not least, let’s briefly ignore the very long history of seven-day weeks and imagine if the week had a different number of days (but with years still the same length and leap years still occurring on the same schedule). What would the calendar repetition cycle look like then?
Calendar cycle for a six-day week. (As much as everyone complains about Mondays, I’m opting to ditch Wednesday for symmetry’s sake.)
6-day week: If each week were six days long, then a common year would consist of 60 weeks plus five days (since 
, and a leap year would be exactly 61 weeks long (
). If in “Year 1” of the cycle January 1 falls on a Monday, then the next year will start with a Sunday, and the one after that with a Saturday (i.e., the opposite progression from what happens with seven-day weeks). The calendar cycle would only be eight years long, with only two types of leap year calendars occurring . . . until a leap year is skipped at the turn of the century, and then two other leap year calendars are in the cycle for the next 100 years.
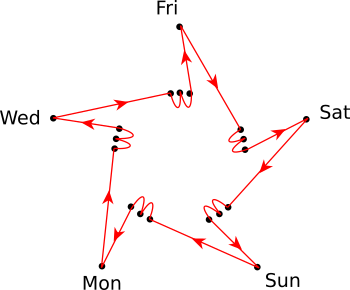
Calendar cycle for a five-day week. (Again appealing to symmetry arguments, we’ll drop Tuesday and Thursday.)
5-day week: If each week were five days long, then a common year would be exactly 73 weeks long (mathematically, 
), while a leap year would be 73 weeks and a day (
). Any given common year would recur thrice in a row, followed by a leap year that also starts on the same day of the week, after which the next four years would all start on the following day of the week. All 10 types of calendars would occur, and the full cycle would take 20 years before it repeated.
Calendar cycle for an eight-day week. (Let’s make three-day weekends the rule rather than the exception, and we’ll follow the pattern of naming days of the week after bodies in our solar system.) For this one, I’ve switched colors at each leap year to make it easier to follow the lines through the pattern.
8-day week: If each week were eight days long, then a common year would be 48 weeks plus 5 days long (since 
). There would be 16 different calendars that occur in a 32-year cycle; as with the seven-day week and the five-day week case, each leap year occurs once and each common year occurs three times. Interestingly, the three repetitions of a common year calendar occur in close succession, with just three years in between — then don’t recur again until the next cycle (26 years later).
At this point, we’ve pretty well exhausted the calendar question we started out with, so I’ll bring things to a close, but for more fun pattern games and/or pretty pictures along these same lines (pun intended), check out some of the following:
- multiplication table polygons (mathrecreation)
- star polygons (mathrecreation, Wolfram Mathworld)
- geometric string art